Chapter 23: Are the stars much closer than believed?
The most indigestible aspect of the heliocentric theory is, undoubtedly, its implications for the extravagant sizes and remoteness of the stars. In any event, the idea that some of the visible stars in our skies would be located several thousands of light years away is simply ludicrous. Let's pause for a moment to consider what exactly the distance known as "1 LIGHT YEAR" implies - and how it translates in units of kilometers:
1 AU (average Earth-Sun distance) = 149 597 870.7 km (or roughly 149.6 Mkm)
1 LIGHT YEAR = 63241.1 AU = 9 460 730 472 580.8 km (or roughly 9.46 TRILLION kilometers!)
Ever since the Copernican theory came along, the apparent angular diameter of the stars as perceived from Earth by the human eye has been one of the most hotly debated issues of astronomy. Since the theory implied that the stars were hugely more distant than previously believed, it became imperative for the Copernican advocates to find some justification for the apparent size of the distant stars. This, because the stars in our skies (especially the largest or closest “first-magnitude stars”) appear to our naked eye to be far too large, if they were to be as formidably distant as currently claimed.
Let me use a real photograph of our night skies to illustrate the issue at hand. Note how the apparent diameter of the star Sirius seems to be roughly the same size, or even perhaps a tad larger, than that of Jupiter - as viewed from Earth by a naked-eye observer:

Image source and date: Tom Wildoner - October 8, 2015
That’s right: if we were to trust our own eyes (something we may all probably need to learn anew!), we would have to conclude that Sirius is about 8834 times larger than the Sun. That is, of course, assuming that Sirius is truly as distant as currently claimed - i.e. 8.6 light years (or 543865 times further away than the Sun). Yes, that's more than HALF A MILLION times more distant than our Sun (which subtends only about 0.5° in our sky)!
Our Moon also subtends about 0.5° in our sky. Now, take a good look at the above photograph - and compare the visible sizes of the Moon and Sirius. Does Sirius appear to be several million times smaller than the Moon - the angular diameter of which is similar to our Sun? Of course not.
Moreover, we would have to accept that most of the bigger stars in our skies are hundreds of times larger than the Sun. As it is, this is precisely what Tycho Brahe held as the most unacceptable notion put forth by the Copernicans: the sheer absurdity of the gigantic star sizes and distances that their novel model implied. Over the last centuries, volumes of science literature have sought to explain the apparent optical aberration of the observed star sizes. Ironically, it was that epochal technological advancement - the telescope - that provided the Copernicans with some "optical justification” (or, if you will, another sort of 'aberration of light excuse') for the pesky problem, courtesy of Astronomer Royal George Airy (yes, the very same guy who disproved James Bradley's "aberration of starlight"!...)
Today, young astronomers are taught that the observed dimensions of the points of light emanating from the stars are totally spurious because they are artificially enlarged as they traverse Earth’s atmosphere. A phenomenon known as 'diffraction' would cause the angular diameter of the stars to appear much larger than they are in reality. Here’s a paragraph from the Wikipedia regarding the so-called “Airy disk” diffraction phenomenon:
"AIRY DISK : The resolution of optical devices is limited by diffraction. So even the most perfect lens can’t quite generate a point image at its focus, but instead there is a bright central pattern now called the Airy disk, surrounded by concentric rings comprising an Airy pattern. The size of the Airy disk depends on the light wavelength and the size of the aperture. John Herschel had previously described the phenomenon, but Airy was the first to explain it theoretically. This was a key argument in refuting one of the last remaining arguments for absolute geocentrism: the giant star argument. Tycho Brahe and Giovanni Battista Riccioli pointed out that the lack of stellar parallax detectable at the time entailed that stars were a huge distance away. But the naked eye and the early telescopes with small apertures seemed to show that stars were disks of a certain size. This would imply that the stars were many times larger than our sun (they were not aware of supergiant or hypergiant stars, but some were calculated to be even larger than the size of the whole universe estimated at the time). However, the disk appearances of the stars were spurious: they were not actually seeing stellar images, but Airy disks. With modern telescopes, even with those having the largest magnification, the images of almost all stars correctly appear as mere points of light.”
In short, Airy claimed that we cannot trust our eyes when it comes to judging the angular diameters of the stars, since points of light are distorted / enlarged as they traverse Earth’s atmosphere. However, there’s an obvious problem with Airy’s theory: why then wouldn’t the points of light emanating from our planets (e.g. Venus or Jupiter) be similarly affected? Doesn’t the light emanating from our planets also traverse our atmosphere - much like that emitted by the stars? Of course it does. Tycho Brahe’s estimate of the angular diameter of Vega (a so-called “first-magnitude star”) was 120 arcseconds, or only about 16 times smaller than the angular diameter subtended by the Sun (1920 arcseconds). Now, many of you will probably scoff at Brahe's “generous” estimate of the angular size of Vega, so here’s a comparative graphic I made to illustrate what this would look like:

BIG DOT = the Sun. SMALL DOT = a 1st magnitude star such as Vega, visually 16 times smaller than the Sun, according to Tycho Brahe.
Indeed, the small dot is only 16 times smaller than the big dot (representing the Sun). All in all, it doesn’t look too different from what we can see in reality with our own eyes, does it? As you can see (with your own eyes), Tycho Brahe's contention (that 1st magnitude stars such as Vega are only about 16X smaller than the sun) would seem quite reasonable after all. Now consider this: Vega (the second-brightest star in the northern celestial hemisphere, after Arcturus) is currently believed to be 25 light years away, i.e. 1 583 000 times (yes, more than 1.5 million times!) more distant than our Sun. Yet, Vega’s diameter is estimated to be only about 2.3 times larger than that of the Sun. Now, if I enlarged the big dot in my above comparative graphic 2.3 times, then scaled it down 1.5 million times, would it possibly be visible from Earth with any sort of telescope - let alone with our naked eyes? Now, Vega's intrinsic luminosity (or 'wattage', if you will) is officially reckoned to be 40X stronger than our Sun's; yet, even if this were true (i.e. if the gauging of stellar luminosity is correct), this would still fall short of explaining how Vega can be one of the brightest stars in our skies. I trust that you'll start appreciating the problems posed by the alleged, ginormous stellar distances. But it gets worse.
HOW CAN WE SEE SO MANY STARS WITH OUR NAKED EYES?
1 AU (average Earth-Sun distance) = 149 597 870.7 km (or roughly 149.6 Mkm)
1 Light Year = 9 460 730 472 580.8 km (or roughly 63241 AU !)
It is a matter of historical record that Tycho Brahe rejected the idea of the implied Copernican star sizes and distances. This conviction may be phrased in a question such as, “why would Alpha Centauri (our nearmost star) be so enormously more distant than, say, Saturn?” To be sure, this still-unanswered question was precisely what most bothered Tycho Brahe about the heliocentric Copernican theory.
“In the absence of any observed stellar parallax, Tycho scoffed for example at the absurdity of the distance and the sizes of the fixed stars that the Copernican system required: Then the stars of the third magnitude which are one minute in diameter will necessarily be equal to the entire annual orb [of the earth], that is, they would comprise in their diameter 2284 semidiameters of the earth. They will be distant by about 7850000 of the same semidiameters. What will we say of the stars of first magnitude, of which some reach two, some almost three minutes of visible diameter? And what if, in addition, the eighth sphere were removed higher, so that the annual motion of the earth vanished entirely [and was no longer perceptible] from there? Deduce these things geometrically if you like, and you will see how many absurdities (not to mention others) accompany this assumption [of the motion of the earth] by inference.”
Here is the inescapable question our world's astronomers must answer: how can so many stars possibly be visible to our unaided eyes?
If we consider the distances currently claimed for one of our brighter stars, Deneb (a.k.a. Alpha Cygni), the whole affair becomes well and truly outlandish. Deneb is said to be a good 200 times larger than our Sun - but we are also told that it is a whopping 2600 LY away from our eyes - or about 164 426 800 AU!
Well, that's over 164 MILLION times(!) further away than the Sun - or if you prefer, 24 598 249 280 000 000 km... And yet:
"Deneb is one of the brightest stars we can see with the naked eye." "Night Sky: Look Northeast For Deneb" - by Steven Glazier
“A blue-white supergiant, Deneb is also one of the most luminous stars. However, its exact distance (and hence luminosity) has been difficult to calculate; it is estimated to be somewhere between 55,000 and 196,000 times as luminous as the Sun.” “Deneb” - on Wikipedia
Pardon me? "Between 55000 and 196000 times as luminous as the Sun"?... With such a vast range of luminosity estimates and 'error margins', one may suspect that they are no more than wild guesses. Besides, could these formidable luminosity estimates just be a way of "justifying" the untinkable stellar distances that the Copernican model requires? And what sort of otherworldly physics would cause a star to shine 196000X brighter than our Sun? Didn't Sir Isaac tell us that the laws of physics are the same throughout the universe? The above Wikipedia page for star Deneb goes on to say that...
“One 2008 calculation using the Hipparcos data (gathered by ESA’s Hipparcos satellite) puts the most likely distance (to Deneb) at 1550 light-years, with an uncertainty of only around 10%.”
Yet, some modern planetariums have Deneb at a distance of 3227 light years, i.e. over twice as distant! Do the stellar distance estimates of our world’s astronomers ever agree with each other? Is star Deneb 1550, or 2600 - or 3227 light years away? Evidently, no one seems to know with any decent degree of precision! I, for one, grew up with the notion that astronomy was far more exacting than this. Virtually nothing adds up with these claimed star distances and luminosities - or the wildly conflicting estimates of the same. They are all, as TV-celebrity Carl Sagan liked to say, “extraordinary claims that require extraordinary evidence”. It should thus come as no surprise that - as we shall see further on - several independent astronomers have, in later years, vigorously questioned NASA and ESA (the European Space Agency) over their claimed star distances published in their official tables and catalogues.
At this point, you (the reader) will probably ask yourself: "Can the TYCHOS model provide any rational argument in support of the notion that the stars would be much closer than currently believed?" The answer to this question is "yes indeed". Here follows the how and why of this confident assertion.
THE TYCHOS MODEL'S "42633-reduction FACTOR"
As we have seen, in the TYCHOS model, Earth only moves by 14036 km every year - or by 7018 km every 6 months.
Of course, star distances have always been measured and computed by astronomers under the assumption that Earth moves around the Sun. They assume that Earth's orbital diameter is 299 200 000 km (or almost 300 million kilometers). Hence, they will 'take a picture' of a nearby star "X" (say, on June 21). Then, after six months (December 21) they 'take another picture' of star "X". They then look at how much star "X" has moved in relation to the 'fixed stars' (i.e. the far more distant background stars) and, with a simple trigonometry calculus, they compute the distance between the Earth and star "X".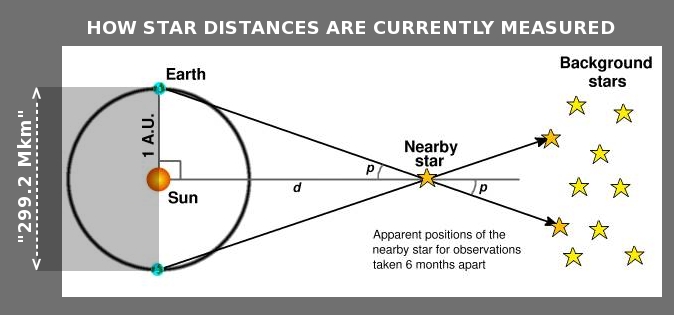
Now, if Earth does NOT move laterally every six months by 299.2 million km - but only by 7018 km (as stipulated in the TYCHOS model) - it follows that the currently-accepted star distances are ALL inflated by a factor of:
299 200 000 ÷ 7018 ≈ 42633
This will be our reduction factor for all the stellar distances listed in official star catalogues.
This also means that, in the TYCHOS, the distance unit known as “1 Light Year” corresponds to less than 1.5 AU :
9 460 730 472 580.8 km (i.e. one “light year”) / 42633 ≈ 1.4834 AU
Let's now put our TYCHOS reduction factor to the test - and see how close Proxima Centauri (our very nearmost star) would be; officially, Proxima is said to be about 4.25 LY away. In the TYCHOS, Proxima would thus be located about 6.3 AU away from Earth :
4.25LY X 1.4834 ≈ 6.3 AU
This is rather interesting, for this TYCHOS-computed distance (6.3 AU) to Proxima would place our nearmost star at a distance roughly 'midway between' Jupiter (4.2 AU) and Saturn (8.5 AU). Note however that Proxima is not located in the same plane as our solar system – but some 62° ‘below’ it. Also, consider that Proxima is reckoned to be a 'red dwarf' (by far the most common star type in our universe) which are notoriously quite dim - due to their intrinsically low luminosity.

Undoubtedly, Tycho Brahe would be most satisfied with that, since his primary objection to the Copernican model was that the stars would have to be “absurdly large and distant” - and that there would have to be a most improbable, enormous void between Saturn and our nearmost stars. In fact, Tycho Brahe’s expert opinion was that the stars were “located just beyond Saturn and of reasonable size”.
“It was one of Tycho Brahe’s principal objections to Copernican heliocentrism that in order for it to be compatible with the lack of observable stellar parallax, there would have to be an enormous and unlikely void between the orbit of Saturn (then the most distant known planet) and the eighth sphere (the fixed stars).” source: "Parallax" - on Wikipedia”
We shall now further use star Proxima as a 'test bed' for another important aspect of the present discourse; namely, that of the perceived telescopic size of stellar disks. As all astronomers will know, it is believed today that the perceived angular diameters of the stars (as viewed telescopically) are spurious, due to assorted diffraction phenomena which would affect telescope lenses - causing the stars to appear, artificially, far larger than they are in actuality (see "Airy Disk" on Wikipedia).
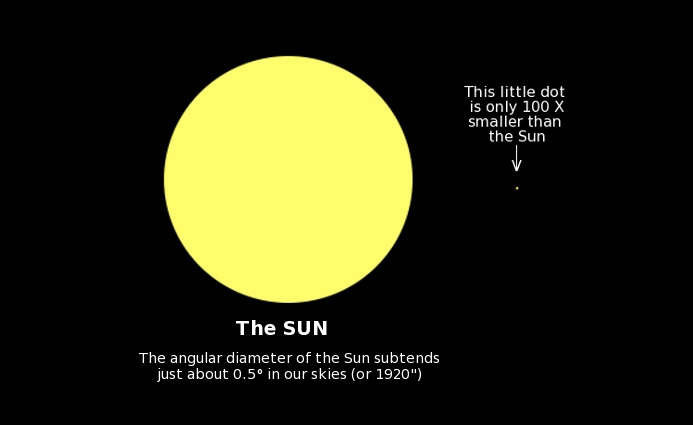
Proxima’s officially-estimated “true” angular diameter is 0.001” arcseconds (although it appears to be MUCH larger in our telescopes). Since the Sun’s observed angular diameter is 1920" arcseconds, this means that Proxima's angular diameter is reckoned to be 1 920 000 times (or almost 2 MILLION times) smaller than the Sun's! To put this into perspective, my below graphic shows how an object only 100 X smaller than the Sun would look like - in our skies. Well, imagine if that little dot wasn’t just 100 times – but as much as 2 MILLION times smaller... Give it a good thought - and let it sink in.
Proxima's actual diameter is estimated - by today's astronomers - to be 1/7th that of our Sun; its distance from our Solar System, as we saw earlier, is officially reckoned to be ca. 4.25 light years - or 268775 AU (i.e. 268775 X further away than our Sun). This, because - as their reasoning goes: 1920” / 268775 ≈ 0.007” / 7 ≈ 0.001" (which, of course, is an absurdly small value - whichever way you look at it!)
Now, is Proxima perhaps an exceptionally bright / luminous star? Well, no - not according to officialdom. Here’s what we may read on the Wikipedia with regards to Proxima's luminosity:
“(Proxima’s) total luminosity over all wavelengths is 0.17% that of the Sun, although when observed in the wavelengths of visible light the eye is most sensitive to, it is only 0.0056% as luminous as the Sun.” "Proxima Centauri" - Wikipedia
In other words, the official data is telling us that Proxima, our very nearmost star…
- Is 7 X smaller than our Sun
- Is located 268775 X further away than our Sun
- Is FAR, FAR dimmer (less luminous) than our Sun
- Has a “true” angular diameter almost 2 MILLION X smaller than our Sun
You may thus rightly wonder how Proxima could then possibly be visible at all (in ANY earthly telescopes)...
On the other hand, if the TYCHOS' 42633 factor for star distances is correct, we see that Proxima's true angular diameter (as seen in our telescopes) would amount to a more reasonable 42.633" arcseconds (42633 X 0.001 = 42.633) - which would make it only 45 times smaller than the Sun's undisputed 1920" angular diameter (1920" / 42.633" ≈ 45). Thus, if the TYCHOS' proposed Earth-Proxima distance of 6.3 AU is correct, this would indeed make Proxima about 7 times smaller than the Sun (45 / 6.3 ≈ 7.1) - in excellent accordance with official data! Let's now briefly see how this same calculus works out, as applied to Sirius, our largest star (as discussed in Chapter 6):
Officially, Sirius is reckoned to be 8.7 Light Years away. As we apply our 42633 reduction factor, the Earth-Sirius distance in the TYCHOS would be about 12.9AU (8.7LY X 1.4834 = 12.9AU). The angular diameter of Sirius (as stated in the Wikipedia) is 0.005936″. As we multiply this value by 42633, we obtain 0.005936" X 42633 ≈ 253". Now, Sirius is estimated to be 1.7 times larger than the Sun, so let's first divide this value by 1.7 : 253 / 1.7 = 148.82" (which would be the expected angular diameter of Sirius - IF it were the same size of the Sun). As we finally divide the Sun's undisputed angular diameter (of 1920") by this value, we obtain: 1920 / 148.82 ≈ 12.9.
Earlier on we saw that Vega, according to Tycho Brahe's expert judgment, subtended 1/16th of the diameter of the Sun. Again, Brahe's main objection to the Copernican model was that the stars could not be so hugely distant - or else they would ALL have to be hugely larger than our Sun. Brahe reckoned instead that the (true) respective diameters of the visible stars were more homogeneous, i.e. only somewhat larger or smaller than our Sun (as opposed to dozens, hundreds, or even thousands of times larger). One must admit that, from a purely statistical viewpoint, this makes perfect sense - for why would there be so many "giant and supergiant" stars in our 'cosmic neighborhood'? To be sure, the Wikipedia tells us that "giant stars have radii up to a few hundred times the Sun and luminosities between 10 and a few thousand times that of the Sun", whereas the radii of supergiant stars can be "in excess of 1,000 solar radii and (can have) luminosities from about 1,000 to over a million times the Sun." The question is: why would that be?
But let's stay focused on our closer and most well-known stars - such as star Vega. We shall now take a comparative look at the estimated angular diameter of Vega - as proposed by Brahe, Galileo and our modern astronomers. Remember that Vega is reckoned today to be only 2.3X larger than the Sun - and to be located 'only' 25 light years away from the Earth.
TYCHO BRAHE's estimate of VEGA's angular diameter: 120" arcseconds
GALILEO GALILEI's estimate of VEGA's angular diameter: 5" arcseconds
MODERN ASTRONOMERS' estimate of VEGA's angular diameter: 0.0029" arcseconds
We see that today, modern astronomers estimate the angular diameter of VEGA to be:
- 1724X smaller than GALILEO's estimate
and
- 41379X smaller than BRAHE's estimate (or very close to the TYCHOS' 42633 reduction factor).
Let's now see if we may at least 'rescue' the notion that VEGA is 2.3X larger than the sun - as currently estimated.
VEGA is claimed to be 25.04 light years away. In the TYCHOS model, 1 light year = 1.4834 AU (i.e. 42633X less than 1 light year).
Hence, in the TYCHOS model, the Earth-->VEGA distance would amount to: 25.04 X 1.4834 = 37.144 AU.
Remember now that Tycho Brahe estimated VEGA's angular diameter to be about 16X smaller than our sun.
Well, if Vega is truly 37.144X more distant than the Sun (and appears to be 16X smaller), it would indeed be ca. 2.3X larger than the sun :
37.144/16 = 2.3215
In summary :
Tycho Brahe may have been right all along about the visible size of Vega (and the stars in general).
My proposed reduction factor of 42633 (for the currently-reckoned star distances) would seem to agree with Brahe's estimates.
If the stars are 42633 X closer than thought, it doesn't necessarily follow that their diameters are 42633 X smaller than currently estimated.
In any event, should the stars be much closer than currently believed, this would certainly help explain why we can see so many stars with our naked eyes - and why first magnitude stars (e.g. Sirius or Vega) can appear in our skies of similar size as, for instance, Jupiter. To be sure, further study is needed in the field of optical astronomy, a branch of human knowledge rife with controversy still today. In fact, the long-debated question of the perceived telescopic star disk sizes and how they would be affected by various phenomena (e.g. lens diffraction, "Airy disk", assorted optical issues, etc.) is far from being a settled matter. The same goes for the notion of redshift and blueshift being doppler effects currently used to determine whether stars are receding from or approaching our Solar System - but more about that in Chapter 26.
IS OUR MOON WAVING GOOD-BYE TO MOTHER EARTH?
Modern astronomers will tell you that “the Moon recedes from Earth each year by (a little less than) 4 centimeters”. We shall now see how the Tychos model can account for - and thus dismantle - the rather alarming notion that our Moon would be, slowly but surely, "waving goodbye" to Mother Earth!
“The Moon is gradually receding from the Earth, at a rate of about 4 cm per year. This is caused by a transfer of Earth's rotational momentum to the Moon's orbital momentum as tidal friction slows the Earth's rotation.” "WHAT WILL BE THE FATE OF OUR MOON?" - Physlink.com
“Although the moon’s distance from earth varies each month because of its eccentric orbit, the moon’s mean distance from Earth is nonetheless increasing at the rate of about 3.8 centimeters (1.5 inches) per year. That’s about the rate that fingernails grow.” "WAYWARD MOON RECEDING FROM EARTH" - EarthSky.org
According to the TYCHOS, the Moon is not receding from Earth and is not going to vanish in space; we shall now see why the Moon's "4-cm-per-year recession" is yet another illusory conclusion drawn by Copernican astronomers who are, of course, unaware of the existence of the 25344-year PVP orbit. Hence, their computations related to the Moon’s apsidal oscillations will always fail to account for this ‘secular revolution’ of the Earth-Moon system. As they measure (against the background stars) this minute “4-cm annual recession” of the Moon, they will conclude that “our Moon is slowly drifting away from Earth”.
However, we know that the Moon-Earth distance is constantly oscillating back and forth (i.e. cyclically approaching and receding from the Earth). As we saw in Chapter 13, the Moon's orbit oscillates back and forth by 42108km (a value which we shall call the "MMAO" - i.e. "the Moon's Maximal Apsidal Oscillation"). So could the secular drift of the MMAO (over a Great Year of 25344 solar years) possibly be responsible for what astronomers interpret as an annual "4-cm recession of the Moon"? Let's see if this might be the case:
If we consider that the Earth-Moon system completes a full 360° revolution in 25344 years, we may envision how the MMAO (as its spatial orientation remains 'fixed' to the Moon's orbit) will slowly revolve ONCE in relation to the Earth in 25344 years. We may thus calculate by how much the MMAO would appear to 'drift' annually (as viewed from the Earth and in relation to the stars):
42108km / 25344y = 1.66km-per-year (representing the amount that the Moon will appear to recede from us annually - due to the slow, secular 'precession' of the MMAO around Earth)
Now, astronomers will be using their 'long-established' star distances as a benchmark to gauge the fluctuating Moon-Earth distances (i.e. with instruments calibrated to the officially-estimated stellar distances). However, we just saw that the stars may be 42633 times closer than currently believed. So let's divide the above value by 42633 - and see what we obtain:
1.66km / 42633 = 0.0000389km = 3.89cm (i.e. the amount that astronomers reckon to be "the Moon's annual recession rate"!)
In conclusion, the Moon is - thankfully - not parting from us anytime soon. What astromomers are "seeing" is just the very slow, 25344-year secular precession of the MMAO - given by the tranquil 1-mph-revolution of the Earth-Moon system around the PVP orbit. In our current epoch, the MMAO's oscillation is evidently in its 'receding phase', but over time, there will be an 'approaching phase' which will bring things back to normal - in the good tradition of the wondrously stable and reliable "Swiss clockwork" known as our Solar System. We shall now see how some other well-known astronomical data (related to stellar motions) go to support my proposed “42633 reduction factor”.
ABOUT OUR RELATIVE SPEED VIS-A-VIS THE STARS
The velocity value of ≈20 km/s (or more precisely, 19.4 km/s) keeps popping up all over astronomy literature. As shown in the below-quoted papers, there appears to be some sort of general consensus regarding this velocity value, although its actual meaning is rather nebulous. “A 20 km/s speed in relation to what?”
Nonetheless, it appears this value is meant to represent the “perceived average relative speed” between our solar system and the stars (as computed under the tenets of the Copernican theory and its implied Earth > Stars distances).
“…The solar system itself has a velocity of 20km/s with respect to the local standard of rest of nearby stars…”
“The average radial velocity of the stars is of the order of 20 km per second”.
— "The Motion of the Stars" - by J. S. Plaskett (1928)
“The Sun’s peculiar velocity is 20 km/s at an angle of about 45 degrees from the galactic centre towards the constellation Hercules.”
— "Spiral Galaxies" - by Dmitri Pogosian (2018)
“The Sun is moving towards Lambda Herculis at 20km/s. This speed is in a frame of rest if the other stars were all standing still.”
— "What is the speed of the Solar System?" - by Deborah Scherrer, Hao Tai and J. Todd Hoeksema (2017)
“The speed of the Sun towards the solar apex is about 20 km/s. This speed is not to be confused with the orbital speed of the Sun around the Galactic center, which is about 220 km/s [or 800.000 km/h] and is included in the movement of the Local Standard of Rest.”
— "Solar apex" - on Wikipedia”
Here we have a more detailed account as to exactly how a ca. 20 km/s motion between the Sun and the stars was determined:

The Paris Observatory provides the more exacting figure of 19.4 km/s - or a displacement of "about 4 AU/year":
“Solar apex: The point on the celestial sphere toward which the Sun is apparently moving relative to the Local Standard of Rest. Its position, in the constellation Hercules is approximately R.A. 18h, Dec. +30°, close to the star Vega. The velocity of this motion is estimated to be about 19.4 km/sec (or about 4 AU/year). As a result of this motion, stars seem to be converging toward a point in the opposite direction, the solar antapex.”
“Antapex: The direction in the sky away from which the Sun seems to be moving (at a speed of 19.4 km/s) relative to general field stars in the Galaxy.”
In the interest of accuracy, we should probably use this 19.4 km/s value, as it appears to be our modern-day, currently-accepted estimate. So let us convert this value from km/s to km/h.
19.4 km/s X 3600 = 69840 km/h (This velocity is essentially described as representing the motion of the Solar system relative to the stars).
Now, remember that in the TYCHOS, Earth’s orbital velocity is deemed to be 1.6 km/h. This would constitute, of course, our 'proper motion' in relation to the stars. Hence, if the stars are much closer to us than currently believed, their perceived velocity should be divided by our 42633 reduction factor. So let us do just that - and see what we obtain:
69840 km/h / 42633 ≈ 1.638 km/h
Wow! This is very close to 1.601169 km/h – i.e. Earth’s orbital speed as proposed by the TYCHOS model!
Next, let us apply our 42633 reduction factor on that "4 AU/year" displacement estimate - as provided by the Paris Observatory:
4 AU = 149 600 000 km X 4 = 598 400 000 km
598 400 000 km / 42633 = 14036 km!!!
Wow again - or Good Heavens, you might say! This is exactly our EAM, i.e. Earth's Annual Motion as estimated in the TYCHOS model!
In conclusion, the “general velocity perceived to exist between the stars and our Solar System” (ca. 19.4 km/s) would seem to support both of the TYCHOS model’s "boldest" - yet most fundamental assertions:
• Earth moves around space at the very tranquil speed of 1.6 km/h.
• The stars are about 42633 X closer than currently estimated.
ABOUT THE SOLAR ANTAPEX AND THE SOLAR APEX
In the last few centuries, astronomers have dedicated humongous efforts to determine the spatial progression & direction of the Sun - in relation to our surrounding stars. What they call the "solar antapex" is the point in the sky from which the Sun appears to be receding - whereas the "solar apex" is the point in the sky towards which the Sun appears to be approaching. To make a long story short, it has now finally been determined that the Sun is receding from a celestial point (at RA 6h28m - roughly in the direction of star Sirius) and approaching a celestial point (at RA 18h28m - roughly in direction of star Vega). Source: SOLAR APEX - at Wikiwand
Well, this would be in most excellent accordance with the TYCHOS model - which has the Sun moving precisely in such manner. My below graphic illustrates that, in the TYCHOS, the Sun would indeed (over a 12672-year period, i.e. half a TYCHOS Great Year) be MOVING AWAY from RA:6h28m - and MOVING TOWARDS RA:18h28m. In this respect, the TYCHOS model fully agrees with the observed / computed spatial progression and direction of the Sun's motion - from its antapex to its apex. Et sic probatio (or, if you will, Q.E.D.):

In the next chapter, we shall see how Earth's claimed translational velocity (i.e. its supposed hypersonic orbital speed of ca. 30km/s - or 107226km/h - as of Copernican theory) has never been experimentally verified nor confirmed. This is a hard fact which no earnest astronomer can deny - yet relativists will unfailingly roll their eyes and tell you that "Einstein has long explained why the Earth's spatial velocity is impossible to measure!"...